Artikeln innehåller nedan en översättning av en text ursprungligen publicerad på www.allinone.nu och författad av min äldre broder Carl. R. Wern. Den handlar om tre 2000-åriga geometriska problem som har varit olösta: 1) Vinkelns tredelning, 2) Cirkelns kvadratur, och 3) Kubens fördubbling. Teoretiskt saknar de tre problemen en generell lösning när passare och en omärkt linjal är de enda tillåtna hjälpmedlen.

Pi-dagen & Internationella Matematikdagen 2023.03.14 valdes som artikelns publiceringsdatum därför att det är lika omöjligt att räkna fram ett exakt siffervärde för talet Pi som att rittekniskt uppdela med omärkt linjal och passare en godtycklig vinkel i tre exakt lika delar. Arkimedes, antikens störste matematiker vars porträtt nedan och på frontsidan målades ca 1620 av Domenico Fetti i Mantua, var intresserad av båda utmaningarna. Han presenterade ett sätt att beräkna Pi med hög noggrannhet, men någon redovisning finns varken från honom eller från någon annan av ett sätt att klara vinkelns tredelning med den hårfina noggrannhet som Carl presterat.

Intresset för prestationen har redan resulterat i artiklar publicerade av tidskrifterna Ny Teknik och Teknikhistoria. Tre generationer efter Carls examen som ingenjör från Stockholms Tekniska Institut önskar han inför dess 100-årsjubileum 2024 och sitt eget 100-årsjubileum 2025 väcka mediaintresse för vikten av att ingenjörsskolor har inspirerande matematiklärare. 

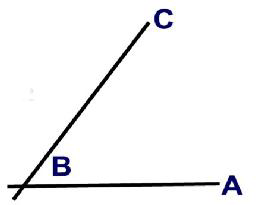
Fig. A

1. Vinkelns tredelning - att dela en vinkel i 3 lika delar
    https://sv.wikipedia.org/wiki/Vinkelns_tredelning

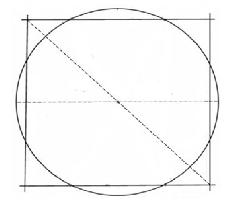
Fig. B

2. Cirkelns kvadratur - att konstruera en kvadrat med samma area som en cirkel.
    https://sv.wikipedia.org/wiki/Cirkelns_kvadratur

+    =     

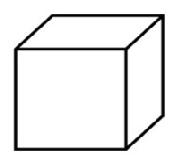Fig. C

3. Kubens fördubbling - att konstruera en kub som har summavolymen av två  lika stora kuber.
https://sv.wikipedia.org/wiki/deliska_problemet

Carl R. Wern beskriver nedan hur dessa tre problem löses på ett generellt sätt med mycket hög noggrannhet.

VINKELNS TREDELNING

Att dela en vinkel i två lika delar är inget problem. Det är väl känt hur detta kan ske  såsom visat i FIG 1. Men att dela en vinkel i tre lika delar har varit ett olöst problem i mer än 2000 år. 

Hur tredelas en valfri vinkel inom intervallet 0°-180°?

En Columbi-ägg-lösning är att använda två cirklar. Om en av dem har en radie = 1, då ska den andra ha en radie specificerad som R = 2 sin (V°/12). Denna Columbi-ägg-ekvation är exakt. 

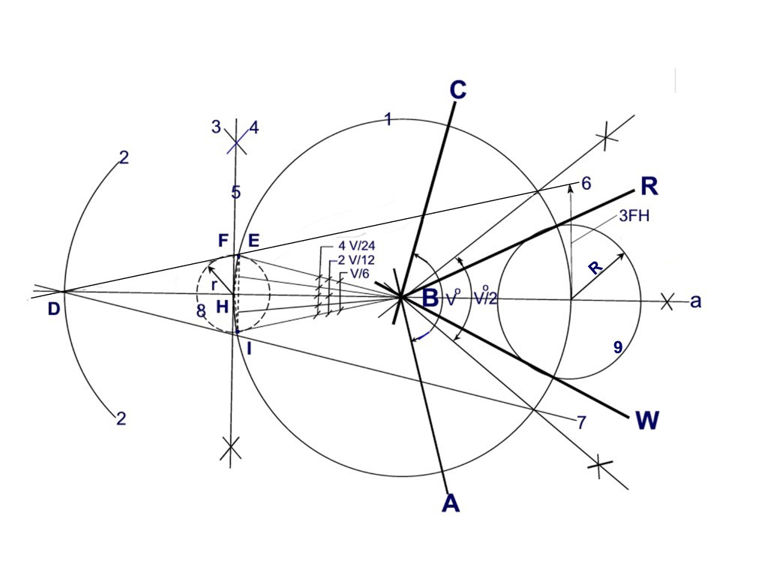
                                                                                        FIG. 1
Matematisk och teknisk lösning
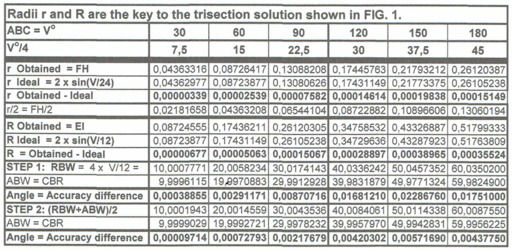
En valfri vinkel ABC inom intervallet 0°-180° delas i fyra lika delar på ett välkänt sätt. Tredelningen utförs inom linjerna 6 och 7. Cirkeln 1 antages ha en radie = 1. Cirkeln 8 ges en radie r = FH. Det uppnådda resultatet FH för radien r = sin (V°/4)/(2 + cos (V°/4)) och det ideala resultatet FH för radien r = 2 sin (V°/24). Cirkeln 9 ges en radie R = EI för att dela vinkeln ABC i tre lika delar så exakt som det kan göras med givna verktyg. Tabellen nedan visar uppnådd precision för r, R and (V°/3).

Tredelningens precision
Ett exakt resultat kan ej uppnås för värdet på Pi och för alla trigonometriska tabellvärden. I likkhet därmed är tredelningen inte exakt men så perfekt som möjligt med givna verktyg. Tabellen nedan visar den otroligt lilla skillnaden mellan uppnådda och ideala siffervärden för cirkelradierna r and R.

Definierat läge för punkten E

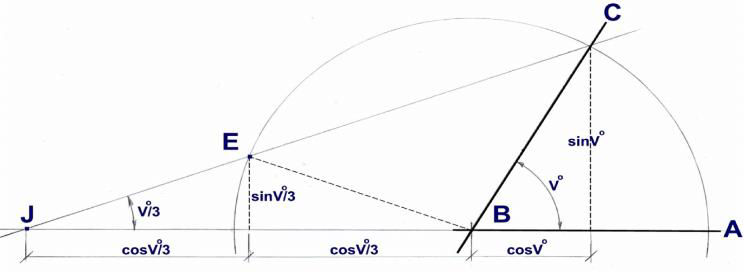
Fig. 2

Punkt E ovan hittas såsom visat i FIG. 2 inom feltoleransen när en passare används.
Dess läge är anvisat av Werns lösning som är relaterad till följande ekvation.

sin V°/3 = cos V°/3 x sin V°/(cos V° + 2 x cos V°/3)

Kontrolldiagram

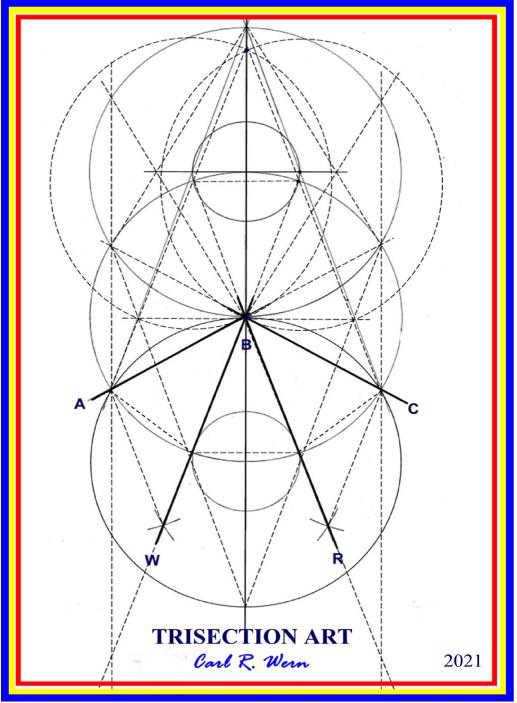
Streckade linjer är tillagda för att visa överensstämmelsen med resultaten av de inkomplettera lösningar som Hippokrates och Archimedes anvisade.

Kommentarer:

 
1. Reinhard Atzbach, Animation - Trisection 1 
https://geogebra.org/classic/enrdzqaf 
2. Reinhard Atzbach, Animation - Trisection 2, .
https://geogebra.org/classic/auasjdh8
3. Åke Tegengren, Matematisk Kommentar 1 Mathematisk Kommentar 1
www.allinone.nu/ABC/Kommentar1.pdf
4. Åke Tegengren, Matematisk Kommentar 1 Mathematical Comments 1
www.allinone.nu/ABC/Comments1.pdf
5. Ny Teknik Article 1
www.allinone.nu/ABC/1.NyTeknik.pdf
6. Ny Teknik Article 2
www.allinone.nu/ABC/2.NyTeknik.pdf
7. Teknik Historia Article 3
www.allinone.nu/ABC/3.TeknikHistoria.pdf
8. Aditya Khavanekar News, Copy from internet
www.allinone.nu/ABC/AncientProblems.pdf

Allmänt

9. https://cut-the-knot.org/pythagoras/archi.shtml
10. https://onlinekalkylatorn.se

Allmän historik

Vinkelns tredelning är sedan drygt tvåtusen år ett geometriskt problem som är känt att sakna en allmängiltig lösning när passare och en omärkt linjal är de enda tillåtna hjälpmedlen.

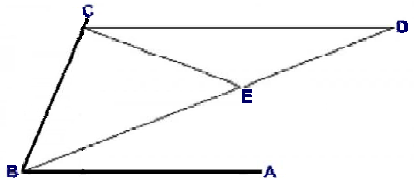
Fig. 3

Hippokrates var den störste av antikens läkare och mycket intresserad av matematik.
Han föreslog en lösning visad i FIG. 3.
Lösningen är inkomplett eftersom det har saknats en allmängiltig anvisning för att finna på vinkelbenet BD den passande punkten E som bildar de likbenta trianglarna BCE & CED utan andra hjälpmedel än en omärkt linjal och en passare.

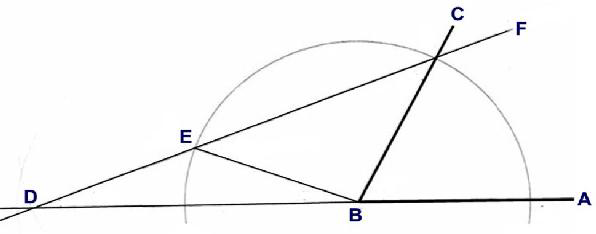
Fig. 4

Arkimedes, den störste av antikens matematiker, var också fysiker, ingenjör, uppfinnare och astronom.
Hans förslag till en lösning visas i Fig 4.
Också den lösningen är inkomplett eftersom en allmängiltig anvisning har saknats för att finna på cirkelperiferin den passande punkten E som bildar de likbenta trianglarna BDE och BCE med endast de tillåtna hjälpmedlen.

Den franske matematikern Pierre Wantzel presenterade 1837 ett matematiskt bevis på att det finns teoretiskt med de tillåtna hjälpmedlen ingen allmängiltig lösning på det tvåtusenåriga problemet med vinkelns tredelning.

2. Cirkelns kvadratur

Allmänt
Här beskrivs en allmänt användbar lösning med de givna hjälpmedlen.

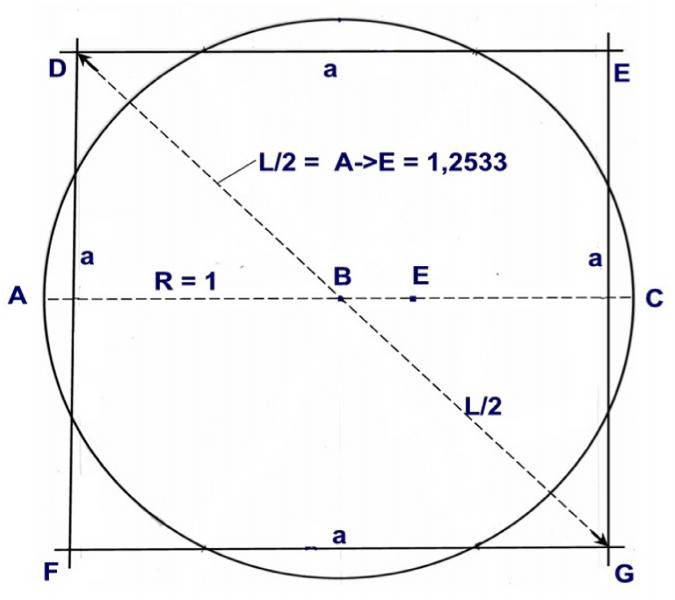
Fig. 5

Kvadratens yta ska vara lika med cirkelns yta
Cirkelns yta = R x R x pi = pi om R = 1.
Kvadratens yta = a x a = a²
a² = pi, a = 1,7724539 = kvadratens sida a.

Kvadratens diagonallängd DB = L/2, DG = L
L² = a² + a² = pi + pi        pi = 3,141592654…
L² = 3,1416 + 3,1416 = 6,2832
L = 2,5066 och L/2 = 1,2533

Sök rittekniskt positionen för punkten L/2.
Dela cirkelradie B tIll C i 4 lika delar.
Då blir A till E = 1 + 0,25 = 1,25
Gör A till E = L/2 = 1,25 vid uppritning

FIG. 6 visar slutlig lösning vid uppritning av kvadratens yta = cirkelns yta.

ANM
Differensen 1,2533 - 1,2500 = 0,0033 är i stort sett betydelselös. Noll går ej att uppnå. Ökad noggranhet sker om man från punkt D2 drar cirkel 9 till höger strax bredvid punkt 1/8 & E
Se anvisning i) nedan.

Lösning för cirkelns kvadratur.

Fig. 6

Anvisning för lösning av cirkelns kvadratur med de tillåtna hjälpmedlen.
Använd passare och en omärkt linjal.

1. Dra en rak linje 1 från A till C.
2. Slå med passare från punkt B/1 en cirkel 2.
3. Slå med passaren från punkt D cirkel 3 genom B1
4. Slå med passaren från punkt G cirkel 4 genom B1.
5. Dra en rak linje 5 genom dubbla punkterna 2/4.
6. Slå med passare från B/1 två korta cirkelbågar 6.
7. Slå med passare från F/1 två korta cirkelbågar 7.
8. Dra en rak linje 8 genom båda punkterna 6/7.
9. Slå från D2 två korta halvcirkelbågar 9 strax till höger om punkt 1/8 & E för ökad noggrannhet.
10. Slå från G2 med samma båge 9 båge 10
11. Slå från B1 med samma båge 4 cirkelbågar 11.
12. Dra en rak linje 12 genom dubbla punkterna 9/10.
13. Slå från H2 en halvcirkelbåge 13 genom B1.
14. Slå från I2 en halvcirkelbåge 14 genom B1.
15. Dra en rak linje 15 från B genom 3/13 och 14/4.
    Dra en rak linje 16 från B genom 3/14 och 13/4.
16. Dra en rak linje 17 genom punkterna J/11 och K/11.
    Dra en rak linje 18 genom punkterna J och L.
    Dra en rak linje 19 genom punkterna K och M.
    Dra en rak linje 20 genom punkterna L och M.

Kvadratens yta är nu likvärdigt med cirkelns yta

ANM
Kvadratens och cirkelns ytor är nu lika stora så perfekt som det kan bli gjort med givna regler.

Kubens Fördubbling

Problemet är att konstruera en kub som har summavolymen av två lika stora kuber.

Kub A	+	Kub B	=	Kub C
		Fig. 7

KUBENS VOLYM
Kub A och B. Sida a = 1.
Kub A = a³ = 1 och Kub B = a³ = 1
Kub A + B = 2 och kub C = d³
d³ = 2     d = 1,259921
Skapa en sidlängd som motsvarar d.

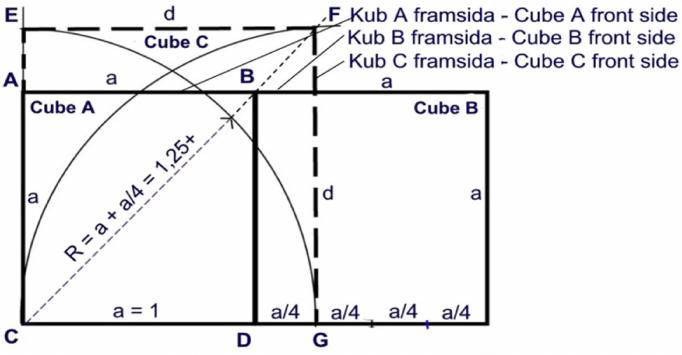
Fig. 8

Anvisning för lösning av problemet.
Använd passare och en omärkt linjal.
a. Rita upp framsidan för 2 lika stora kuber, A och B.
b. Använd passaren och dela sida a för kub B nedtill i 4 lika delar, 4 x a/4 med känd metod.
c. Dra en rak streckad linje upp från C genom B.
d. Använd passaren & dra från C en cirkel G till E.
e. Dra med samma cirkel från G en cirkel C till F.
f. Dra en streckad linje d från E till F och från G-F.

ANM
Kub C har nu summavolymen av kuberna A & B så perfekt som det går att göra med givna medel.
Med värdet d = 1,25 blir differensen 0,009921 som är knappt märkbar.