This article contains below a translation of a text originally published on www.allinone.nu and written by my older brother Carl R. Wern. It is about three 2000-year old geometric problems that have been unsolved: 1. Angle trisection, 2. Squaring the circle, 3. Doubling the cube.  Theoretically, these problems lack a general solution when a compass and an unmarked ruler are the only permitted tools.

Pi-day & International Mathematics Day 2023.03.14 was chosen as the publication date of the article because it is as impossible to calculate an exact numerical value for the number Pi as it is to technically divide with an unmarked ruler and a compass an arbitrary angle into three exactly equal parts. Archimedes of Syracuse (the portrait shown below and at the front page was painted about 1620 by Domenico Fetti in Mantua) became interested in both challenges and presented a way to calculate Pi with high accuracy but there is no account, either from him or anyone else, of a way to handle the trisection of the angle with the razor-thin accuracy achieved by Carl.

The interest in the achievement has already resulted in articles published by the magazines Ny Teknik and Teknikhistoria. Three generations after Carl's degree as an engineer from the Stockholm Institute of Technology, he wishes, ahead of its 100th anniversary in 2024 and his own 100th anniversary in 2025, to arouse media interest in the importance of engineering schools having inspiring mathematics teachers. 

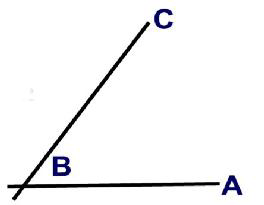
Fig. A

A. Angle trisection - to split an angle in 3 equal parts.
    https://en.wikipedia.org/wiki/Angle_trisection

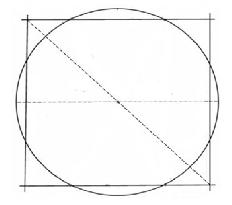
Fig. B

B. Squaring the circle - to create a square with the same area as a circle.
    https://en.wikipedia.org/wiki/Squaring_the_circle

+    =     

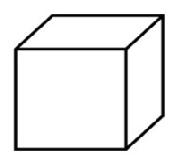Fig. C

C. Doubling the cube - to create a cube that has the sum volume of two equal sized cubes.
https://en.wikipedia.org/wiki/Doubling_the_cube

Carl R. Wern describes below how these three problems are solved in a general way and with very high accuracy.

ANGLE TRISECTION

To split an angle into two equal parts is no problem. It is well known how this can be done as shown in FIG 1.  But to split an angle into three equal parts has been an unsolved problem in more than 2000 years. 

How to trisect any angle ABC within the interval 0°-180°

A Columbi egg solution is to use two circles. If one of them has a radius = 1, then the other would have a radius specified as R = 2 sin (V°/12). This Columbi egg equation is exact.  

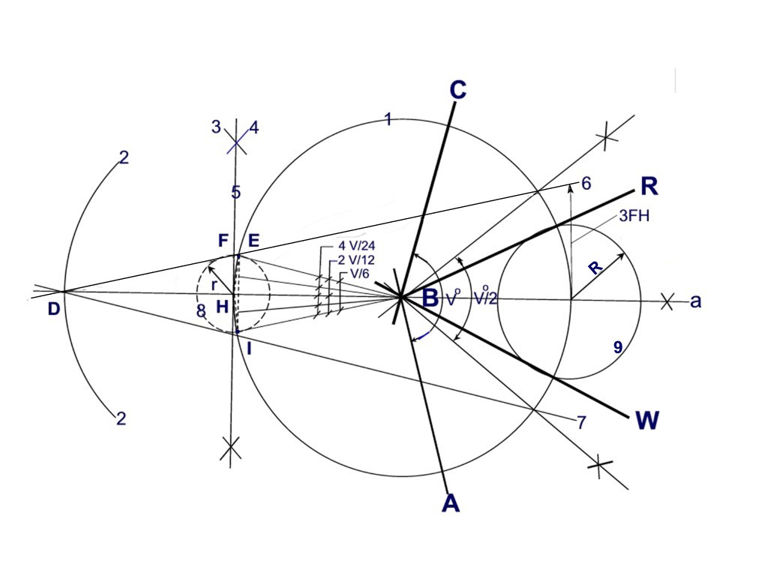
                                             Fig. 1

Mathematical & technical solution
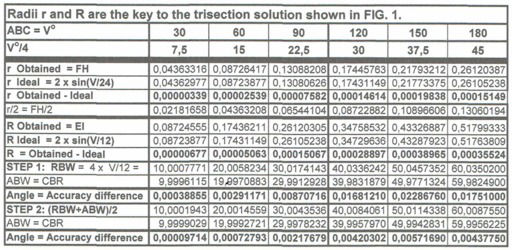
Any angle ABC within the interval 0°-180° is divided into four qual parts in a well known way. The trisection is made within the lines 6 and 7. The circle 1 is here assumed to have a radius = 1. Then the circle 8 is given a radius r = FH. While the obtained result FH for the radius r = sin (V°/4)/(2 + cos (V°/4)), the ideal result FH for the radius r = 2 sin (V°/24). The circle 9 is given a radius R = EI to split the angle ABC into three equal parts as exact as it can be made with the given tools. The table below shows the obtained precision for r, R and (V°/3).

The trisection precision
An exact result can not be achieved for the value of Pi and for all the trigonometric values. Likewise, the presented trisection is not exact but it is as perfect as possible with the given tools. The table below shows the unbelievable little difference between obtained and ideal figures for the circle radii r and R.

Defined position of point E

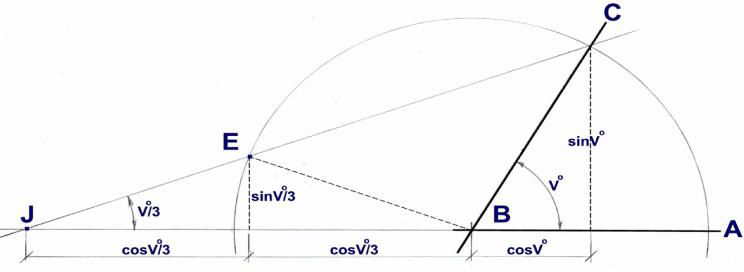
Fig. 2

Point E above is found as shown by FIG. 2 within the fault tolerance when a compass is used.
Its position is devised by Wern's solution that is related to the following equation. 
sin V°/3 = cos V°/3 x sin V°/(cos V° + 2 x cosV°/3)

Control Chart

Dotted lines are added to show consistency with the results of the incomplete solutions devised by Hippokrates and Archimedes.

Comments:

 
1. Reinhard Atzbach, Animation - Trisection 1 
https://geogebra.org/classic/enrdzqaf 
2. Reinhard Atzbach, Animation - Trisection 2, .
https://geogebra.org/classic/auasjdh8
3. Åke Tegengren, Matematisk Kommentar
www.allinone.nu/ABC/Kommentar1.pdf
4. Åke Tegengren, Mathematical Comments 
www.allinone.nu/ABC/Comments1.pdf
5. Ny Teknik Article 1
www.allinone.nu/ABC/1.NyTeknik.pdf
6. Ny Teknik Article 2
www.allinone.nu/ABC/2.NyTeknik.pdf
7. Teknik Historia Article 3
www.allinone.nu/ABC/3.TeknikHistoria.pdf
8. Aditya Khavanekar News, Copy from internet
www.allinone.nu/ABC/AncientProblems.pdf

General

9. Angle Trisection by Archimedes of Syracuse                                                                                                                              https://cut-the-knot.org/pythagoras/archi.shtml                                                                                                                      10. Online Calculator                                                                                                                                                                          https://onlinekalkylatorn.se 

General history

Angle trisection has been a geometric problem for more than two thousand years. It is known to lack a general solution when a compass and an unmarked ruler are the only permitted tools.

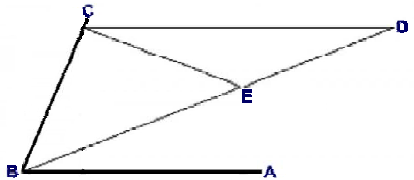
Fig. 3

Hippokrates was the greatest of the ancient physicians and very interested in mathematics.
He proposed a solutlon shown in FIG. 3. The solution is incomplete because there has been no general instruction to find on the angIe leg BD the fitting point E creating the isosceles triangles BCE & CED without other tools than an unmarked ruler and a compass.

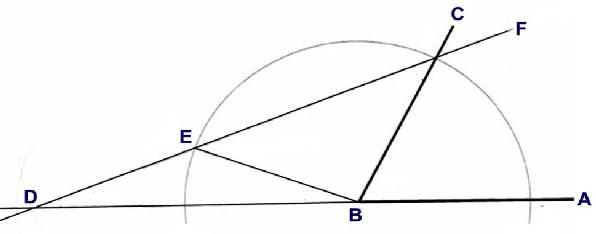
Fig. 4

Archimedes, the greatest of the ancient mathematicians, was also a physicist, engineer, inventor, and astronomer. He proposed a solution shown in Fig. 4. This solution is also incomplete because it lacks a general instruction to find on the periphery the fitting point E which forms the isosceles triangles BDE and BCE with only the permitted tools.

The French mathematician Pierre Wantzel presented In 1837 a mathematical proof that there is in theory with the permitted tools no general solution to the two-thousand-year-old problem of the trisection of the angIe.

2. Squaring the circle

General
Carl R. Wern describes here a useful solution with the permitted tools

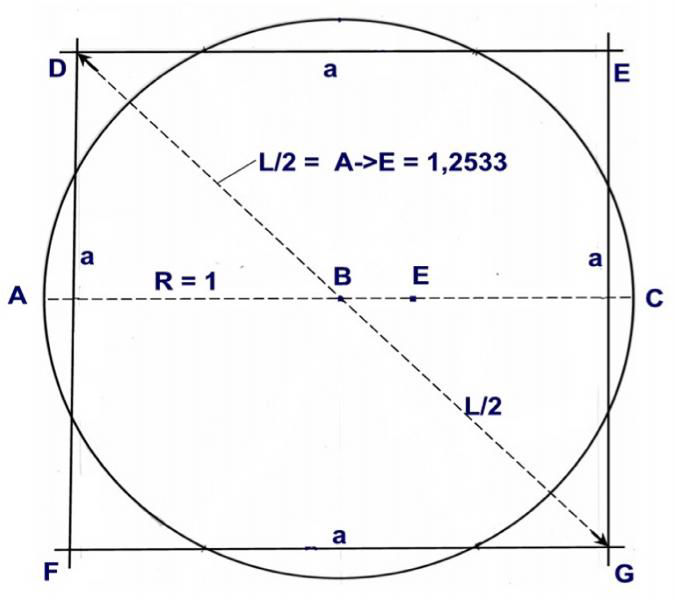
Fig. 5

A square and a circle with equal areas.
Circle area = R x R x pi = pi if R = 1.
Square area = a x a = a²
a² = pi, a = 1,7724539 = square side a.

Square diagonal length DB = L/2, DG = L
L² = a² + a² = pi + pi      pi = 3.141592654…
L² = 3.1416 + 3.1416 = 6.2832
L = 2.5066. L/2 = 1.2533

Find drawing point for L/2
Split circle radius B to C in 4 equal lengths.
Then A to E would be = 1 + 0,25 = 1,25.
Make A to E = L/2 = 1.25 for drawing design

FIG. 6 show the final drawn up solution for the square area = circle area.

NOTE
The difference 1.2533 -1.2500 = 0.0033 is in
general insignificant. Zero is not achievable. Increased accuracy occurs if you draw from point D2 circle 9 to the right just next to point 1/8 & E.
See instruction i) below.

Solution for squaring the circle.

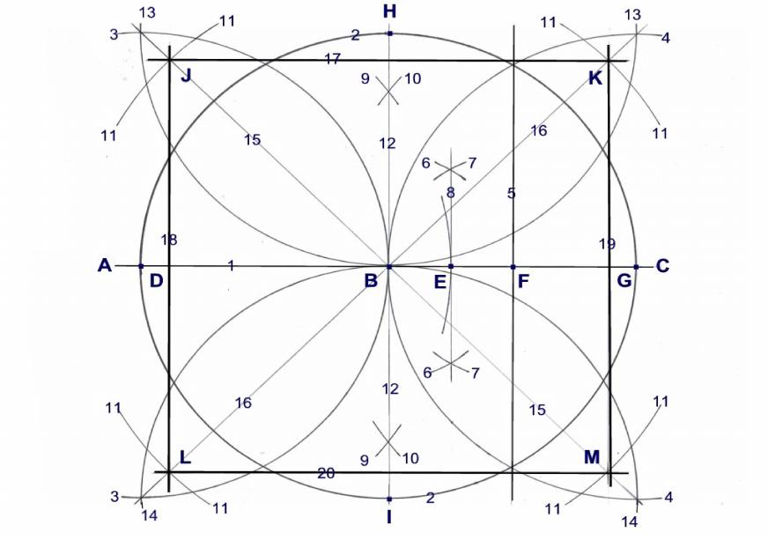
Fig. 6

Instructions for squaring the circle with the permitted tools.
Use a compass and an unmarked ruler.

1. Draw a straight line 1 from A to C.
2. Draw by compass from B/1 a circle 2.
3. Draw by compass from D circle 3 thru B1.
4. Draw by compass from point G circle 4 thru B1.
5. Draw a straight line 5 thru double points 2/4.
6. Draw by compass from B/1 two short arc circles 6.
7. Draw by compass from F/1 two short arc circles 7.
8. Draw a straight line 8 thru both points 6/7.
9. Draw from D2 two short arc circle bows 9 just to the right of point 1/8 & E for increased accuracy.
10. Draw from G2 with same arc 9 thru bow 10.
11. Draw from B1 with same arc 4 arc bow 11.
12. Draw a straight line 12 thru double points 9/10.
13. Draw from H2 a half arc circle bow 13 thru B1.
14. Draw from I2 a half arc circle bow 14 thru B1.
15. Draw a straight line 15 from B thru 3/13 and 14/4.
    Draw a straight line 16 from B thru 3/14 and 13/4.
16. Draw a straight line 17 thru points J/11 and K/11.
    Draw a straight line 18 from B thru points J and L.
    Draw a straight line 19 from B thru points K and M.
    Draw a straight line 20 from B thru points L and M.

The square area is now equivalent to the circle area.

NOTE
The square and the circle areas have now equal size as perfect as it can be done with given tools.

Doubling the Cube

The problem is to create a cube that has the sum volume of two equal-sized cubes.

Cube A	+	Cube B	=	Cube C
		Fig. 7

THE CUBE'S VOLUME
Cube A and B. Side a = 1.
Cube A = a³ = 1 and Cube B = a³ = 1
Cube A + B = 2 and Cube C = d³
d³ = 2     d = 1.259921
Create a length that corresponds to d.

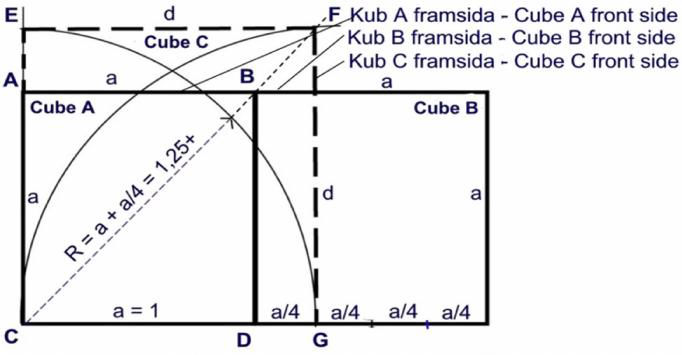
Fig. 8

Instruction for solving the problem.
Use a compass and an unmarked ruler.
a. Draw up front side for 2 equal size cubes, A and B.
b. Use compass and divide side a for cube B at
bottom in 4 equal lengths, 4 x a/4 by known method.
c. Draw a straight dotted line from C thru B.
d. Use compass and draw from C a circle G to E.
e. Use compass and draw from G a circle C to F.
f. Draw a dotted line d from E to F and from G-F.

NOTE
The cube C has now the sum volume of the cubes A & B as perfect as it can be done with permitted tools.
The value d = 1.25 makes the difference 0.009921 that is hardly noticeable.