Just in time for the International Year of Astronomy 2009, it was confirmed that the presumed remains of Nicolaus Copernicus beneath the floor of Frombork cathedral in Poland matched strands of hair found between the pages in a book once owned by him. Like his adventurous contemporary Christopher Columbus, Copernicus pioneered a new perspective on the earth. Honoured as the father of astronomy, he broke with the geocentric cosmology and proposed heliocentric circular orbits for the known planets and the earth.

Several decades later, Johannes Kepler found that the orbits could be accurately described as ellipses and discussed the new cosmology with Galileo Galilei. However, it took some more decades until Isaac Newton made it accepted. He explained the elliptical orbits by means of a theory of gravitation which still serves its purpose after three centuries with all kinds of discoveries in the field of astronomy. Although not predicted by Albert Einstein, his general theory of gravitation is applicable on the cosmic expansion and its apparent acceleration with “dark energy” as the name of a mysterious cause. There is no agreement on its nature!

The author proposes an explanation where the dark energy concept is challenged by a new Wave Theory of Time, hereinafter called WTT. According to the new theory, the accelerated expansion of the cosmos is derivable from an oscillation in the flow of time viewed with light in free space as its measure rather than commonly used time reference sources. These are here a less natural choice because they are based on the atom that does not play a more central role in the cosmic expansion than the earth in the solar system. The observable trajectories of the planets became more logical when the right perspective was chosen and the same goes for the apparent acceleration of the cosmic expansion.

In the simplest chosen WTT model, a wave has a repetition period T and an amplitude that represents a cosmic scale varying sinusoidally with a flow of cosmic time t representing propagating light waves in free space so the light year measure would here be applicable. The cosmic scale is defined by means of a flow of reference time t_r measured by atomic clocks and is expressed as d_t/dt_r. The resulting equation {dt\over dt_r} = {sin \left ( 2 \pi t \over T \right ) } yields {t_r} = \left (T \over 2 \pi \right ) ln \space tan \left(\pi t \over T \right) or {tan \left ( \pi t \over T \right)} = { exp \left ( 2 \pi t_r \over T \right) } and t = { \left( T \over \pi \right)arctan \space exp \left( 2 \pi t_r \over T \right) } so d_t/dt_r ={ sin \left( {2arctan \space exp} { \left( 2πt_r \over T \right) } \right) }. The cosmic time span t_k between the wave peak and a small fraction k of the same is determined by the equation {t_k} = \left( T \over 2 \pi \right) \left( \left( \pi \over 2 \right)– arcsin(k) \space \right). Approximately, k = { \left( 2 \pi t \over T \right) } so tan \left( \pi t \over T \right) = tan \left( k \over 2 \right) or tan \left( πt \over T \right) = {k \over 2}.

However, t_{peak} = {T \over 4} so tan \left( \pi t_{peak} \over T \right) = { tan \left( \pi \over 4 \right) } = {1}, and the reference time span t_r,_k is consequently determined as {t_r,_k} = { \left( T \over 2 \pi \right) \left( ln \space 1 – ln \left( k \over 2 \right) \right) } or {t_r,_k} = \left( T \over 2 \pi \right) ln \left( 2\over k \right).

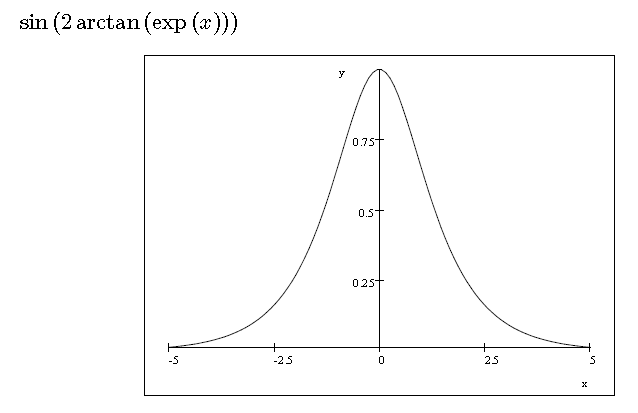The enclosed graph shows an S-shaped curve that is a well-known model for accelerated expansion phenomena. Derived by WTT from a sine wave chosen as the most fundamental form of an oscillation, it predicts how a cosmic expansion scale Y varies with the elapsed expansion time X when this is measured by the common references. As an outcome of known data and straight-forward calculations, the cosmological horizon and the present phase of expansion are found as follows. The equation {d_t \over dt_r} = { sin \left( 2 \space arctan exp \left( 2 \pi t_r \over T \right) \right) } is represented by the simplified expression Y ={ sin( 2arctan(expX)) } so X = { 2 \pi t_r \over T } and a small fraction k of the peak yields X = ln \left( 2 \over k \right). At the cosmological horizon, WTT determines the related fraction k of the peak as equal to 2/137 so the resulting value for X is ln137 or 4.9. The present phase of expansion is determined as corresponding to a fraction k of the peak approximately equal to 1/12, and the resulting value for X is then ln24 or 3.2. The graph shows here an acceleration in the cosmic expansion scale explained by a mathematical model of a time loop rather than a dark energy cause.

In a widely accepted picture of the total energy in the cosmos, about 3/4 is constituted by dark energy and 1/5 by dark matter. Besides challenging the dark energy explanatory concept and consequently questioning that picture, WTT predicts that dark matter contains elementary particles related to the oscillation in the flow of time. In fact, one and the same mathematical model is proposed for connecting gravity and electricity to elementary particles interpreted as time loops with a very low and a very high repetition frequency, respectively. This model makes the so-called large number coincidences derivable and the cosmos more predictable than thought after the discovery of its accelerated expansion. A new cosmic perspective is provided which the following lines will describe more in detail.

Atomic clocks depend as references on the elementary charge e for which a field defined radius r_e is calculated from its characteristic mass m_e, the constant speed c of light in vacuum, and the inverse square law. Applying this law, Newton’s gravitational constant G, and an estimate of the total mass M in the cosmos, it is possible to calculate a field defined cosmic radius r_g that is found to have an order of magnitude close to the observable cosmological horizon. In view of the big bang model, G seems to be very fine-tuned. The well-known equations r_g ={ GM \over c^2 } and r_e ={ e^2 \over m_ec^2 } can be used to express two so-called large number coincidences as {r_g \over r_e } = { \left( M\over m_p \right) ^½ } and { r_g \over r_e } = { e^2 \over Gm_p \space m_e } where m_p is the mass of the proton. They are known as interpretable by antrophic reasoning but can be shown derivable from a WTT equation, r_em_e = { r_gGm_pm_e \over r_ec^2 }, that also is expressed as r_em_e = r_gm_g where m_g represents a very small quantity of rest mass. It is by WTT interpreted as the mass of an elementary particle of the gravitational field and used in another easily derived equation, \left( r_g \over r_e \right)^3\left( m_p \over m_e \right) = { M \over m_g }, where a constant density with expansion as proposed for dark energy is a most useful assumption applied instead on the number of elementary particles of gravitation.

Electromagnetic waves are known to exhibit a constant product of a characteristic length and a characteristic mass according to the equation \lambda m = { h \over c } where λ is the wave length, m is the quantum mass and h is Planck's constant. And the wave nature of an electron or other particle having the mass m and the velocity v is known to be described by the same equation written in a more general form, \lambda m = { h \over v }. WTT proposes then that the equation r_ em_e = r_gm_g indicates a common wave nature of the characteristic masses m_e and m_g, that these are related to a very high and a very low repetition frequency f_e and f_g of respective time loops, and that the well-known equation hf = mc^2 is applicable. The repetition frequency f_e is calculated as {m_ec^2 \over h} = {1.236\ 10^{20} Hz} and the repetition frequency f_g as { m_gc^2 \over h } = { Gm_pm_e \over hr_e } = 5.44\ 10^{-20} Hz. This corresponds to a period T of 580 \space 10^9 years as a measure used below to predict when the cosmic expansion will stop.

As described above, the simplest chosen WTT model predicts the time {t_r,_k} ={ \left( T \over 2 \pi \right) ln \left(2 \over k \right) } between the expansion peak and the fraction k of the same. If { d_t \over dt_r } = { sin \left( 2\pi t \over T \right) } is written as { dS \over dt } = c \space cos(2 \pi f_gt), then { S_{peak} } = { c \over 2 \pi f_g } or { S_{peak} } = { h \over 2 \pi m_gc }. Apart from the fine structure constant \alpha , the classical radius r_e and the mass m_e of the electron are related in the same way, r_e ={ \alpha h \over 2 \pi m_ec }. The above equation r_e m_e = r_g m_g implies that r_g ={ \alpha h \over 2 \pi m_gc } or r_g ={ \alpha \space S_{peak} }. The time span between S_{peak} and the cosmological horizon found at 2r_g or at the S_{peak} fraction 2\alpha is determined as \left( {580 \space 10^9 \over 2πC} \right) ln(137) years where C is a cosmic compression coefficient relating the present scale to the scale at the expansion peak. Equally easy, the time span between the expansion peak and the present stage of expansion is determined as \left( {580 \space 10^9 \over 2πC} \right) ln(2C) years. When the difference between these cosmic time spans is combined with the widely accepted age estimate for the cosmos (13.7 \space 10^9 years) into an equation, C is found to be approximately equal to 12. It is then possible to calculate the time span between the expansion peak and the cosmological horizon as well as the remaining time until the end of the cosmic expansion. The results are 38 \space 10^9 and 24 \space 10^9 years, respectively.

If the time span between the expansion peak and the fraction \alpha of the same is expressed as \left( \alpha ^{-1}r_g \over c \right ) ln(2 \alpha^{-1}), \left( \alpha ^{​-1}r_g \over c \right) { \left(2 \over 3 \right)} {\left(α ^{-1} \over 2 \right) }^{1 \over 2}is a correspondingly expressed approximate estimate quickly found from the classical field model of gravity. These estimates are in close agreement supporting WTT's cosmic perspective in which \alpha is a mathematical constant.

Reference: Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Jonathan Cape, 2004/ Alfred A. Knopf, 2005.

This article was published in 2009 by the Swedish Mathematical Society: MEDLEMSUTSKICKET, pp 69-73.

Se även inledningen till denna artikel -
Ett nytt kosmiskt perspektiv - om mörk energi & mörk materia!samt
Mörk materia, mörk energi och två räta linjer i ett nytt perspektiv!